Over last couple of days, I’ve been working on analyzing a simplistic game that I came up with to talk about risk-reward decisions in multiplayer games. What I thought would lend itself to easy analysis in order to prove a point, however, turned out to be a pretty complex and interesting math problem. Yesterday, I presented my findings for the two-player case. As you’d expect, it gets a lot more complicated when you add a third player; so much so that I didn’t even bother trying to work anything out for a four-player situation.
The first interesting thing to notice is an elaboration on what I said previously, about larger die sizes (and thus a larger range of choices) favoring the player who gets to pick last. When we think about multiplayer games, we can see that the actual concern has to do with the number of choices relative to the number of players; the extreme case would be that in which we have as many players as there are sides on the die. In that case, we know that all numbers will be chosen in the end. Thus, the first player has just as much information as the last, and can therefore choose the best number for himself, meaning that the last player is at the greatest disadvantage.
In the three-player case, it (perhaps surprisingly) turns out that the break-even point is once again that of the standard six-sided die. The first player should choose 4, the second should choose 5 (just as in the two-player game) and the third is now left with no better choice than to pick 1 and hope the other two fail. Thus, the second player has a 1/3 chance of winning outright, the first player will win 1/2 of the 2/3 of the remaining times, thus 1/3 as well… leaving 1/3 for the third player.
However, both the 4- and 5-sided dice grant the first player the greatest advantage and the last player the greatest disadvantage, unlike in the two-player game. The players’ best choices and odds of winning for the 4-sided case are: 3 (41.4%), 2 (31.1%), and 4 (27.5%). For the 5-sided case, they are 4 (39.6%), 3 (35.6%) and 5 (24.8%).
The next interesting question is what the last player’s winning strategies look like. As one might guess, they are qualitatively similar regardless of the die size. Here are tables showing the winning choice for the 6-, 10-, 20- and 40-sided cases. The first two players’ choices run along the two axes, with “1” being at the lower and left edges and the maximum number being in the top and right.
Green represents the most aggressive choice: picking the number one higher than the higher of the two opponents’ picks. Yellow is the middle strategy, namely picking a number one higher than the lower of the two opponents’ picks. Red represents the most defensive strategy, refusing to gamble at all, picking “1” and hoping both others fail.
Worth noting is that the boundaries between regions seem to be straight lines (except perhaps for the green-red boundary – it’s hard to tell), and that the red-yellow border is almost, though not quite orthogonal. What this latter fact implies is that there’s a certain maximum gamble that one should be willing to accept, falling around 35-40%. If both opponents pick numbers right around that edge, it’s better to join them in gambling, but if both go much beyond, or if one tries to play “on the edge” and the other chooses the safe route, the last player is better playing it safe himself.
Okay, but what does best play for the other two players look like? You might guess that, given the boundary we just discussed, both players might want to pick a number around there, but this isn’t quite right.
Instead, recall what we said in the case of the two player game, that the point of minimal advantage to the third player is likely to be on the boundary between two strategies. Now that there are three players, however, there are now three viable strategies for the last player… we might then guess that the optimal strategy for the other two is to pick numbers that place him right on the junction between all three! This turns out to be pretty much the truth.
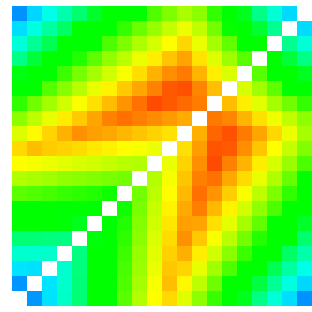
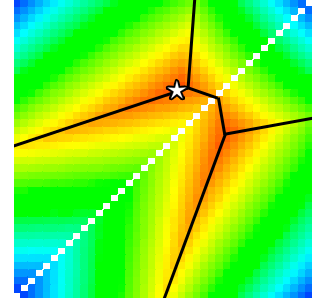If you look at the image up at the top of this post, it shows (for a game with a 20-sided die) the third player’s winning chances for a given combination of choices by the other two; pure red (which doesn’t actually appear, quite) would represent an exactly 1/3 chance for the third player (assuming he makes the right decision), while cooler colors represent better chances of winning. The diagram to the right is similar, but for a 40-sided die.
Looking at the shape, we see that the reddest regions stretch out in spike-like shapes which, intuitively enough, correspond to the boundaries in strategies we found previously. These are marked by black lines on the diagram. The star represents choices of 29 by the first and 23 by the second player, what my program usually gives me as optimal play (though even doing 200,000 iterations, it sometimes moves around a little bit, which illustrates just how close the probabilities are around here). If those are the choices made, the third player should pick 1, and win 38.5% of the time, though he wouldn’t be far off from that picking 24 or 30, either. As it’s easy to see, this is right around the point where a slight shift in choices by the other players could make any of the three strategies the best one.
NOTE: As “perfect play” doesn’t generally exist for games for more than two players, I should clarify that I solved this for the assumption that each player is working to maximize their own odds (rather than minimizing one specific opponent’s odds) and that the players themselves are likewise making this assumption about one another.
And that’s about as much analysis as I want to do on this supposedly “simple” game for now. I’ll make one final post tomorrow, summing everything up and discussing how it might apply to other, more complex games, as well as talking about a couple of possible variations on it that would be even trickier to solve.